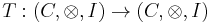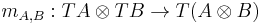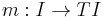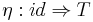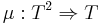Monoidal monad

In category theory, a monoidal monad 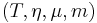$(T,\eta,\mu,m)$ is a monad 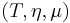$(T,\eta,\mu)$ on a monoidal category 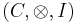$(C,\otimes,I)$ such that the functor

$T:(C,\otimes,I)\to(C,\otimes,I)$

is a lax monoidal functor with

$m_{A,B}:TA\otimes TB\to T(A\otimes B)$

and

$m:I\to TI$

as coherence maps, and the natural transformations

$\eta: id \Rightarrow T$

and

$\mu:T^2\Rightarrow T$

are monoidal natural transformations.

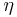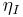By monoidality of $\eta$ , the morphisms $m$ and $\eta_I$ are necessarily equal.

This is equivalent to saying that a monoidal monad is a monad in the 2-category MonCat of monoidal categories, monoidal functors, and monoidal natural transformations.

Properties

The Kleisli category of a monoidal monad has a canonical monoidal structure, induced by the monoidal structure of the monad. The canonical adjunction between $C$ and the Kleisli category is a monoidal adjunction with respect to this monoidal structure.